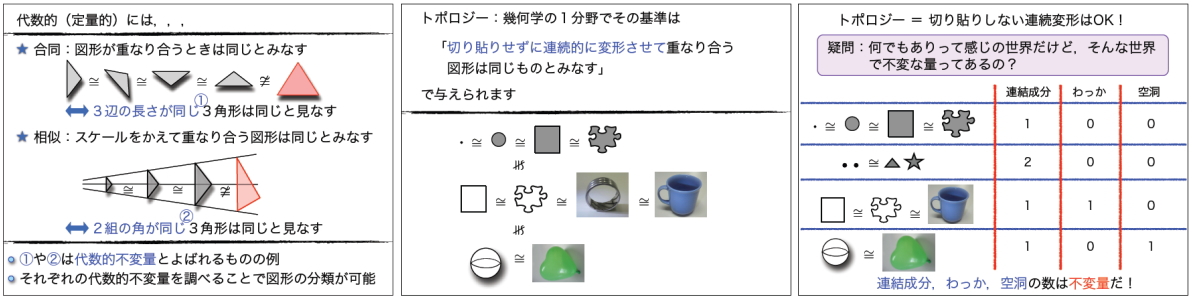
■考え方や定義を変えてみると、モノの見え方が変わってきます。■何かを学問の対象とする場合、対象を分類することを試みますが、分類するためには、「これとこれは同じ」「これとこれは違う」と区別するための基準が必要です。この基準に用いられるものを「不変量」と呼びます。
■三角形が合同であるかどうか判別するためには「３辺の長さ」が不変量として用いられ、三角形が相似であるかどうかを判別するためには「２組の角」が不変量として用いられます。■「ユークリッド幾何学は、合同変換や相似変換によって不変に保たれる性質を調べる学問である」ということになります。■対してトポロジーでは、この基準に用いられる「不変量」が「穴の数」なのです。
★穴の数って何？★
■19世紀末にトポロジーを創設した数学者のアンリ・ポアンカレは 「数学とは、異なるものを同じものと見なす技術である」と言ったそうです。良く分かりませんが、「コーヒーカップとドーナッツは同じだ」と言うことです。■つまり、「コーヒーカップとドーナッツにおいて共通しているものは何か？」を問うのがトポロジーというのです。
■トポロジーの歴史は比較的新しく、18世紀の数学者レオンハルト・オイラーの頃にさかのぼります。オイラーは、川の中の2つの島と両岸との間にかかる7つの橋を1回ずつ渡って回ることはできるかどうかを考察した「ケーニヒスベルクの橋」という問題や、穴の開いていない多面体において「頂点の数−辺の数＋面の数＝2」という「オイラーの多面体定理」が成り立つことなどを発見したことで知られています。
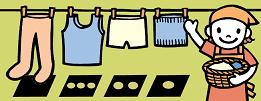
■コーヒーカップとドーナッツだけでなく、おにぎりと鏡餅も、同じモノと見做されます。■分かり易くするために、トポロジーを｢ゴムの幾何学｣などと呼ぶ場合もありますが、仮におにぎりと鏡餅がゴムで出来ているとすれば、ストローを挿して息を吹き込めば膨らみ、最終的には同じ形になります。■また、コーヒーカップとドーナッツも、同じように膨らませれば穴の開いたドーナツのような形になります。■この考え方でいくと、この世にある全ての物体は「膨らましたとき穴が何個開いているか」だけで分類することが出来ます。■短パンは足の出る穴が２つ、シャツは首と両腕の穴が３つ、腹巻きは穴が１つあります。ところがタイツは足のつま先で閉じている。トポロジーからみると、この４つはどれも同じではありません。
■トポロジーの発想とは、形にとらわれずに、それがもっている本質を見極めようとするものであり､図形を変形しても変わらない性質を追究するものだとも言えます。■そのため、正四面体も、正六面体も、球も、本質的に同じものだとトポロジーでは考えます。■一方、ビーチボールと浮き輪は、穴の有無によって本質的に異なるものだととらえます。ビーチボールをどんなにぐにゃぐにゃ変形しても、穴の開いた浮き輪のような形にはできないからです。
★トポロジーって何の役に立つの？★
■マグロは常に泳ぎ続けていなければ死んでしまうので、水族館で飼うには永久に細長く伸びる水槽が必要になります。そこでトポロジー発想で端をなくすことを考えます。■すなわちドーナツ形の水槽を導入すれば、マグロはいつまでも泳ぎ続けることができるようになります。■端をなくせば終わりがなくなるという発想はチェーンソーでも同様です。のこぎりには端があるから、一旦引いたら戻さないといけない。ところが、端をなくして歯を円形にすれば、いつまでも引き続けることができます。■回転寿司、空港の手荷物用ベルトコンベアなども同じ発想に基づいています。
■電力会社は、エネルギーの安定供給確保のために多様なエネルギー源を適切に組み合わせることを目指しており、様々な電源をミックスして電源確保を急いでいますが、そのうちどの電力をどのエリアに送電するか等の送電効率、もしくは、エリア内の幹線が切れた場合に如何にバックアップを図れるようにするか等、実にさまざまな送電の問題を、トポロジーを用いたネットワーク論で解決しようとしています。